Building Abstractions with Procedures Section 2 - Part 1

Section 1.2 Procedures and the Processes They Generate

Exercises in this section of SCIP.

Exercise 1.9. Each of the following two procedures defines a method for adding two positive integers in terms of the procedures inc, which increments its argument by 1, and dec, which decrements its argument by 1.

1
2
3
4
5
6
7
8
9
(define (+ a b)
  (if (= a 0)
      b
      (inc (+ (dec a) b))))

(define (+ a b)
  (if (= a 0)
      b
      (+ (dec a) (inc b))))

Using the substitution model, illustrate the process generated by each procedure in evaluating (+ 4 5). Are these processes iterative or recursive?

Answer 1.9.

For the first process, it is recursive:

1
2
3
4
5
6
7
8
9
=> (+ 4 5)
=> (+ 1 ( + 3 5))
=> (+ 1 (+ 1 (+ 2 5)))
=> ...
=> (+ 1 (+ 1 (+ 1 (+ 1 (5)))))
=> (+ 1 (+ 1 (+ 1 (6))))
=> (+ 1 (+ 1 (7)))
=> ...
=> 9

For the second process, it is iterative:

1
2
3
4
5
6
=> (+ 4 5)
=> (+ 3 6)
=> (+ 2 7)
=> ...
=> (+ 0 8)
=> 8

Exercise 1.10. The following procedure computes a mathematical function called Ackermann’s function.

1
2
3
4
5
6
(define (A x y)
  (cond ((= y 0) 0)
        ((= x 0) (* 2 y))
        ((= y 1) 2)
        (else (A (- x 1)
                 (A x (- y 1))))))

What are the values of the following expressions?

1
2
3
4
5
(A 1 10)

(A 2 4)

(A 3 3)

Consider the following procedures, where A is the procedure defined above:

1
2
3
4
5
(define (f n) (A 0 n))

(define (g n) (A 1 n))

(define (h n) (A 2 n))

Give concise mathematical definitions for the functions computed by the procedures _f_, _g_, and _h_ for positive integer values of _n_.

Answer 1.10.

1
2
3
(A 1 10) = 2^10 = 1024
(A 2 4) = 65536
(A 3 3) = 65536

$$
A(0,n)=f(n)=2n
$$

$$
A(1,n)=g(n)=2^n
$$

$$
A(2,n)=h(n) = \overbrace{(2^{(2^{(2^{…})})})}^{n ~times}
$$

Exercise 1.11. A function f is defined by the rule that f(n) = n if n<3 and f(n) = f(n-1) + 2f(n-2) + 3f(n-3) if n>3. Write a procedure that computes f by means of a recursive process. Write a procedure that computes f by means of an iterative process.

Answer 1.11.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
(define (fun-recursive n)
  (if (< n 3)
  n
  (+ (fun-recursive (- n 1))
     (* 2 (fun-recursive (- n 2)))
     (* 3 (fun-recursive (- n 3)))
     )) 
  )

(define (fun-iter n a b cnt)
     (if (= cnt 0)
            n
            (fun-iter (+ n (* 2 a) (* 3 b)) n a (- cnt 1))
     )
)

(define (fun-iterative n)
    (fun-iter 2 1 0 (- n 2))
)

Exercise 1.12. The following pattern of numbers is called Pascal’s triangle.

1
2
3
4
5
6
				1
			1		1
		1		2		1
	1		3		3		1
1		4		6		4		1
			   ...

The numbers at the edge of the triangle are all 1, and each number inside the triangle is the sum of the two numbers above it. Write a procedure that computes elements of Pascal’s triangle by means of a recursive process.

Answer 1.12.

1
2
3
4
5
6
7
(define (pascal-triangle m n)
    (if (or (= n 1) (= n m))
        1
        (+ (pascal-triangle (- m 1) (- n 1)) 
           (pascal-triangle (- m 1) n))
    )
)

Exercise 1.13. Prove that Fib(n) is the closest integer to $\frac{\phi^{n}}{\sqrt{5}}$, where $\phi=\frac{1 + \sqrt{5}}{2}$.

Answer 1.13.

Theorem 1

$$
Fib(n)=\frac{\phi^n-\psi^n}{\sqrt{5}},\phi=\frac{1+\sqrt{5}}{2}, \psi=\frac{1-\sqrt{5}}{2}
$$

Base Case

$$
Fib(0)=0, Fib(1)=1
$$

Induction Step

\begin{align}
Fib(n-1)+Fib(n-2)&=\frac{(\phi^{n-1}-\psi^{n-1})+(\phi^{n-2}-\psi^{n-2})}{\sqrt{5}}\\
&=\frac{(\phi^{n-1}+\phi^{n-2})-(\psi^{n-1}+\psi^{n-2})}{\sqrt{5}}\end{align}

Meanwhile,

\begin{align}
\phi+1=\frac{3+\sqrt{5}}{2}=\frac{6+2\sqrt{5}}{4}=(\frac{1+\sqrt{5}}{2})^2=\phi^2\\
\psi+1=\frac{3-\sqrt{5}}{2}=\frac{6-2\sqrt{5}}{4}=(\frac{1-\sqrt{5}}{2})^2=\psi^2
\end{align}

Thus,

\begin{align}
Fib(n-1)+Fib(n-2)&=\frac{\phi^{n-2}(\phi+1)-\psi^{n-2}(\psi+1)}{\sqrt{5}}\\
&=\frac{\phi^n-\psi^n}{\sqrt{5}}=Fib(n)
\end{align}

Theorem 2

\begin{align}
\frac{\psi^n}{\sqrt{5}} < \frac{1}{2}
\end{align}

Proof

\begin{align}
\frac{\psi^0}{\sqrt{5}}&\sim0.4472, \frac{\psi^1}{\sqrt{5}}\sim0.2764,…\\
\frac{\psi^n}{\sqrt{5}}&<\frac{1}{2}
\end{align}

Therefore,

\begin{align}
Fib(n) &= \frac{\phi^n-\psi^n}{\sqrt{5}} = \left[\frac{\phi^n-\psi^n}{\sqrt{5}}\right]\\
&=\left[\frac{\phi^n}{\sqrt{5}}\right]
\end{align}

Q.E.D.

Exercise 1.14. Draw the tree illustrating the process generated by the count-change procedure of section 1.2.2 in making change for 11 cents. What are the orders of growth of the space and number of steps used by this process as the amount to be changed increases?

Answer 1.14.

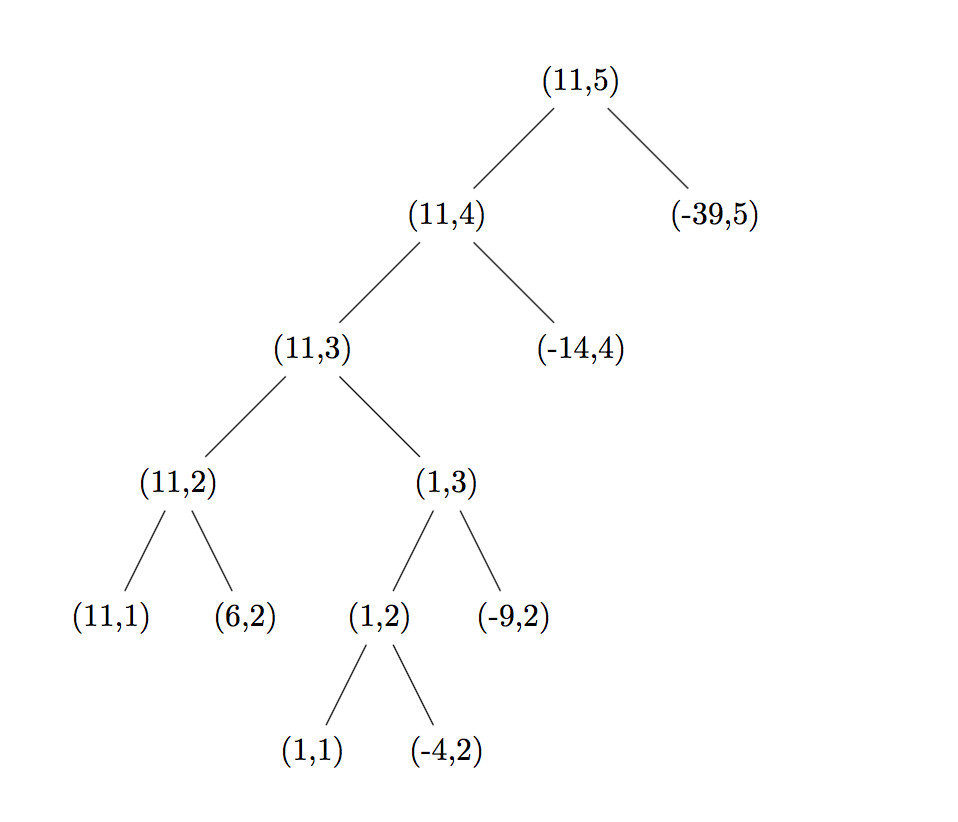
Let the number of kinds of coins: $k$;
Amount of money: $n$;
Denominations: $d_1, d_2, …, d_k$.

Orders of growth of the space

The space required is proportional to the maximum depth of the tree.
Clearly, this means the maximum height is going to be linear in the amount $n$, or $\theta(n)$.

Number of steps

Basic case

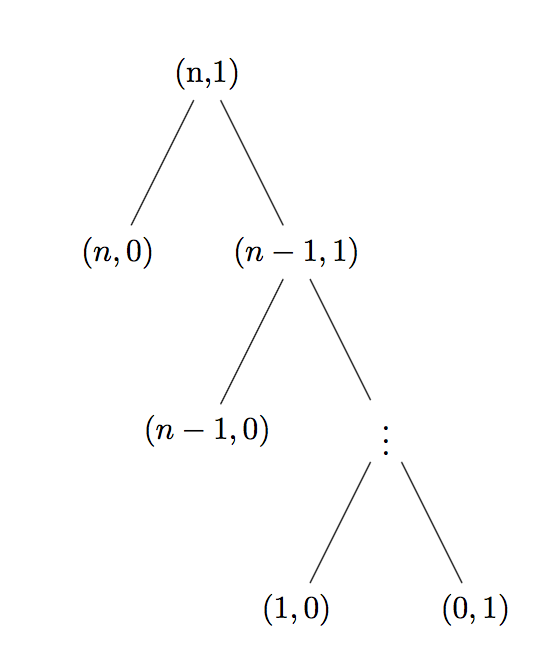
Let see the recursive tree of (cc n 1), which number of steps is defined as $T(n,1)$. Clearly, we can calculate that $T(n,1)=2n+1=\theta(n)$.

Induction step

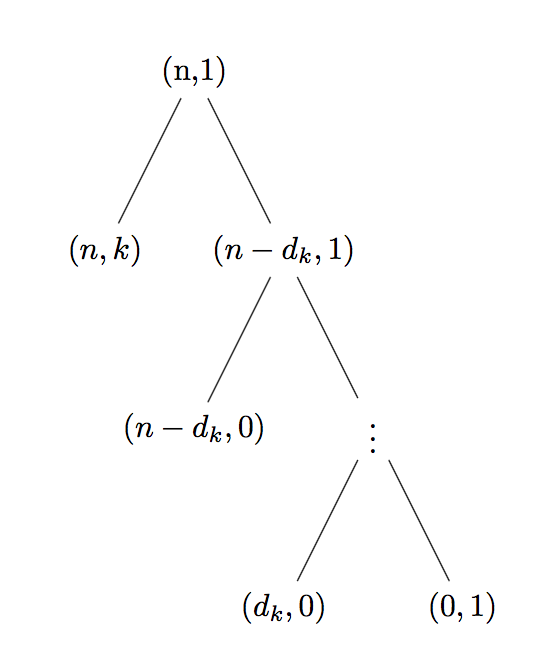
Next, we look at the recursive tree of (cc n k). We have:

$$
T(n,k)=\lfloor \frac{n}{d_k} \rfloor (T(n,k-1)+1)+2
$$

We can expand it further:

\begin{align}
T(n,k)&=\lfloor \frac{n}{d_k} \rfloor (T(n,k-1)+1)+2 \\
&=\lfloor \frac{n}{d_k} \rfloor ((\lfloor \frac{n}{d_k} \rfloor T(n,k-2)+1)+2+1)+2 \\
&= \lfloor \frac{n}{d_k} \rfloor (… (\lfloor \frac{n}{d_k} \rfloor T(n,1)+1)+2 … +1)+2 \\
&= \theta(n^k)
\end{align}

Thus, we have $T(n,5) = \theta(n^5)$.

Exercise 1.15. The sine of an angle (specified in radians) can be computed by making use of the approximation $sin x \approx x$ if $x$ is sufficiently small, and the trigonometric identity

$$
\sin x = 3 \sin \frac{x}{3} - 4 \sin^3 \frac{x}{3}
$$

to reduce the size of the argument of sin. (For purposes of this exercise an angle is considered “sufficiently small” if its magnitude is not greater than 0.1 radians.) These ideas are incorporated in the following procedures:

1
2
3
4
5
6
(define (cube x) (* x x x))
(define (p x) (- (* 3 x) (* 4 (cube x))))
(define (sine angle)
   (if (not (> (abs angle) 0.1))
       angle
       (p (sine (/ angle 3.0)))))

a. How many times is the procedure p applied when (sine 12.15) is evaluated?

b. What is the order of growth in space and number of steps (as a function of $a$) used by the process generated by the sine procedure when (sine a) is evaluated?

Answer 1.15.

a. $\lceil \log_3 \frac{12.15}{0.1} \rceil = 5$.

b. The order of growth in space and number of steps are $\theta(\log n)$.

Exercise 1.16. Design a procedure that evolves an iterative exponentiation process that uses successive squaring and uses a logarithmic number of steps, as does fast-expt. (Hint: Using the observation that $(b^{n/2})^2 = (b^2)^{n/2}$, keep, along with the exponent $n$ and the base $b$, an additional state variable $a$, and define the state transformation in such a way that the product $ab^n$ is unchanged from state to state. At the beginning of the process $a$ is taken to be $1$, and the answer is given by the value of $a$ at the end of the process. In general, the technique of defining an invariant quantity that remains unchanged from state to state is a powerful way to think about the design of iterative algorithms.)

Answer 1.16.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(define (square x)
    (* x x)
)

(define (expt-iter b n a)
    (cond
        ((= n 0) a)
        ((even? n) (expt-iter (square b) (/ n 2) a))
        (else (expt-iter b (- n 1) (* a b)))
    )
)

(define (fast-expt a n)
    (expt-iter a n 1)
)

Exercise 1.17. The exponentiation algorithms in this section are based on performing exponentiation by means of repeated multiplication. In a similar way, one can perform integer multiplication by means of repeated addition. The following multiplication procedure (in which it is assumed that our language can only add, not multiply) is analogous to the expt procedure:

1
2
3
4
(define (* a b)
  (if (= b 0)
      0
      (+ a (* a (- b 1)))))

This algorithm takes a number of steps that is linear in b. Now suppose we include, together with addition, operations double, which doubles an integer, and halve, which divides an (even) integer by $2$. Using these, design a multiplication procedure analogous to fast-expt that uses a logarithmic number of steps.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
(define (double x)
    (+ x x)
)

(define (halve x)
    (/ x 2)
)

(define (mult-iter a b )
    (cond
        ((= b 0) 0)
        ((even? b) (mult-iter (double a) (halve b)))
        (else (+ a (mult-iter a (- b 1) )))
    )
)

(define (fast-mult a b)
    (mult-iter a b)
)

Exercise 1.18. Using the results of exercises 1.16 and 1.17, devise a procedure that generates an iterative process for multiplying two integers in terms of adding, doubling, and halving and uses a logarithmic number of steps.

Answer 1.18.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
(define (double x)
    (+ x x)
)

(define (halve x)
    (/ x 2)
)

(define (fast-mult a b)
    (define (mult-iter a b acc)
        (cond
            ((= b 0) acc)
            ((even? b) (mult-iter (double a) (halve b) acc))
            (else (mult-iter a (- b 1) (+ acc a)))
        )
    )
    (mult-iter a b 0)
)

Exercise 1.19. There is a clever algorithm for computing the Fibonacci numbers in a logarithmic number of steps. Recall the transformation of the state variables $a$ and $b$ in the fib-iter process of section 1.2.2: $a \rightarrow a + b$ and $b \rightarrow a$. Call this transformation $T$, and observe that applying $T$ over and over again $n$ times, starting with $1$ and $0$, produces the pair $Fib(n + 1)$ and $Fib(n)$. In other words, the Fibonacci numbers are produced by applying $T^n$, the $n$th power of the transformation $T$, starting with the pair $(1,0)$. Now consider $T$ to be the special case of $p = 0$ and $q = 1$ in a family of transformations $T_{pq}$, where $T_{pq}$ transforms the pair $(a,b)$ according to $a \leftarrow bq + aq + ap$ and $b \leftarrow bp + aq$. Show that if we apply such a transformation $T_{pq}$ twice, the effect is the same as using a single transformation $T_{p’q’}$ of the same form, and compute $p’$ and $q’$ in terms of $p$ and $q$. This gives us an explicit way to square these transformations, and thus we can compute $T^n$ using successive squaring, as in the fast-expt procedure. Put this all together to complete the following procedure, which runs in a logarithmic number of steps:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(define (fib n)
  (fib-iter 1 0 0 1 n))
(define (fib-iter a b p q count)
  (cond ((= count 0) b)
        ((even? count)
         (fib-iter a
                   b
                   <??>      ; compute p'
                   <??>      ; compute q'
                   (/ count 2)))
        (else (fib-iter (+ (* b q) (* a q) (* a p))
                        (+ (* b p) (* a q))
                        p
                        q
                        (- count 1)))))

Answer 1.19.

Define $a’$ and $b’$ by the definition of the transformation $T_{pq}$:

\begin{align}
a’ &= qb + qa + pa = (p + q)a + qb \\
b’ &= qa + pb
\end{align}

Then, let $a’’$ and $b’’$ be the results of the transformation to $a’$ and $b’$ by applying the transformation once:

\begin{align}
a’’ &= (p + q)a’ + qb’ = (p^2 + 2pq + 2q^2)a + (2pq + q^2)b \\
b’’ &= qa’ + pb’ = (2pq + q^2)a + (p^2 + q^2)b
\end{align}

Thus, we get the transformation to $p$ and $q$:

\begin{align}
p’ &= p^2 + q^2 \\
q’ &= 2pq + q^2
\end{align}